
24GHz帯を使い0.01mmの微小変位や0mからの至近距離を検出できる!
技術解説 上保 徹志
出典 RFワールド No.8 (2009発刊) CQ出版
投稿者注)
本稿は2009年に出版された記事を著者である上保先生に許可を頂いてポストさせて頂いております。
掲載にあたっては執筆時の社会背景やその後の技術動向の推移などに議論があるものとして、敢えて原文に忠実に致しました。
投稿 ピーティーエム株式会社 (以下 PTM と表記)
■はじめに
レーダ(radar)は、電波を使って遠方にある物体を探知し、その物体までの距離や物体の方位、速度を測るものです。このうち本稿は「距離の測定」(測距)に焦点を当てたいと思います。
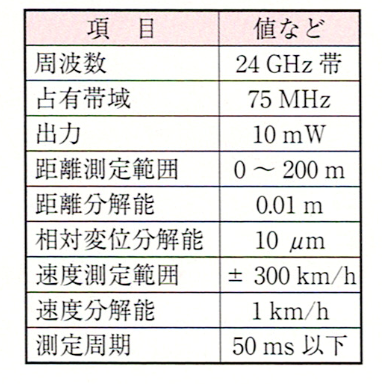
写真1に示すのは、本稿で取り上げる「定在波レーダ」の技術評価用 新型定在波レーダSSRU-2401 [(財)雑賀技術研究所]は、24 GHz(出力10 mW)を使い、0〜200mの範囲を距離分解能0.01m,相対変位分解能10µmで測定することができます。
距離を測定するレーダ
■パルス・レーダとFMCWレーダ
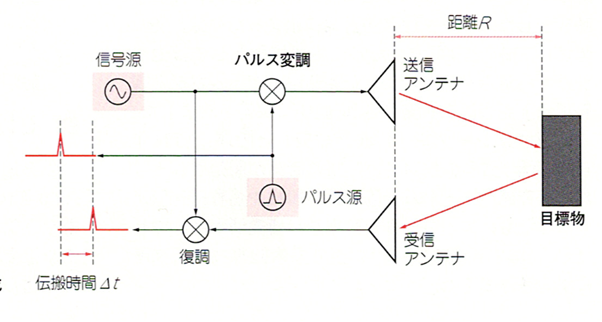
レーダによる測距として、最もよく知られているのはパルス・レーダによる測距(図1)です。これは、物体に向けてパルスを放射し、そのパルスが物体に反射し返ってくるまでの時間から距離を求めるものです。物体までの距離Rは、cを光速として次式で求められます。

ただし、R: 距離[m], Δt: 伝搬時間[s], c: 光速(3×10⁸)[m/s]
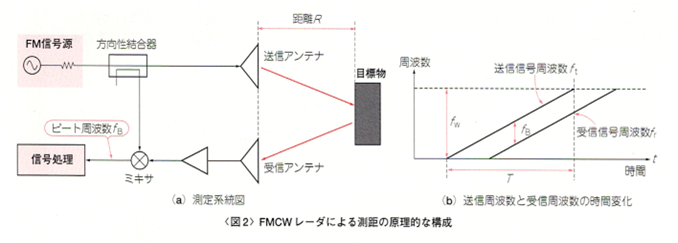
パルス・レーダのほかに測距レーダとして代表的なものにFMCWレーダ(図2)があります。FMCWレーダは周波数変調した連続波を送信し、送信波と反射波の周波数差(ビート周波数)から距離を求める方式です。図2のように周波数を直線的に変化させた場合、物体までの距離Rは、次式で求められます。

ただし、T: 送信時間[s], fB: ビート周波数[Hz], fw: 周波数掃引幅[Hz]
■レーダによる至近距離の測定と問題点
●車載用レーダ
事故防止のためにレーダが車に搭載されるケースが多く見られるようになってきました。


当初、車載レーダは、高速道路走行時に先行車までの距離を計測し、先行車に自動的に追従走行するよう速度を制御する、または、速度に応じた適正な車間距離が確保されていない場合にアラームを出す、などの用途に使用されてきました。
この場合、比較的遠方をレーダによって探知しておけばよいのですが、近年は、予防安全の立場から、遠方よりむしろ車の周囲に近いエリアをレーダで監視することが求められています。
例えば、レーン変更時などにおいて、ドライバの死角にあたる斜め後方に他車やバイクがないかをレーダによって監視する、などといった用途があります。この場合、数m以下の至近距離まで検知できる能力が必要ですが、一般にレーダは至近距離の計測には向いていません。原因の一つは、送信信号の受信系統へのリークがあります。
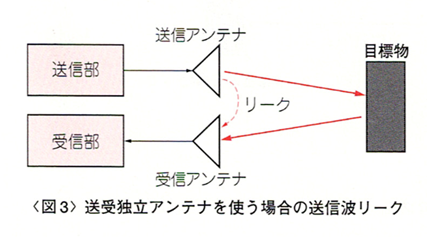
●送信信号の受信系統へのリークが問題
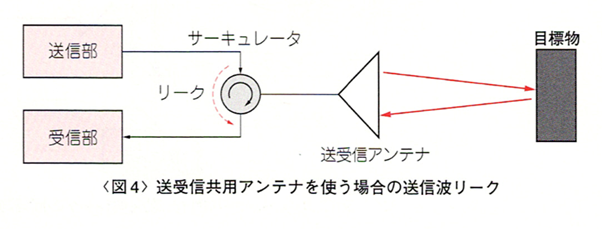
レーダはその構成上、図3のように送信系統と受信系統が極めて近い位置に置かれます。したがって、送信信号が受信系統へリークすることは現実的に避けられません。または、送受信を一つのアンテナで共用する構成もあり、図4のようにサーキュレータによって送信信号と受信信号を分離します。しかし、サーキュレータは送信信号が直接受信系統に入るのを防ぎ、受信系統を飽和や破壊から保護するのが目的であって、受信系統へのリークをなくすことはできません。
このリークは、至近距離にある目標物からの反射波と区別がつかないため、本来あるはずのない目標物(偽目標, false target)が至近距離に検知されてしまいます。しかも受信機の直近で送信を行うため、受信系統へリークする送信信号のレベルは、多くの場合、本来受信すべき目標物からの反射波よりも大きなものとなります。このように、送信信号のリークにより至近距離に現れる偽目標の存在によって、実際に存在する至近距離の目標物の検知が困難となります。
■定在波を利用して近距離測定を可能にする
送信信号の受信系統へのリークをなくすことは現実的に不可能です。しかし、送信信号と受信信号(反射波)を分離しなければ、この問題は根本的になくなります。
そこで、送信信号と受信信号を分離せずその重なりによって生じる定在波を利用して測距する方法について、2000年頃から研究が進められてきました。
■定在波とは
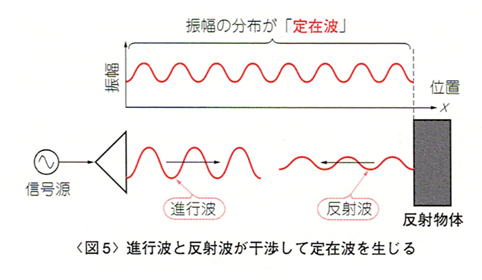
周波数が同じで進行方向の異なる波が重なると定在波が生じます。例えば図5のように信号源と目標物(反射物体)を置くと、その間に定在波が生じます。「信号源と目標物間の距離が、周波数で決まるある特定の距離でなければ定在波は生じない」ということはありません。共振または共鳴現象ならばそのとおりですが、定在波は共振状態か否かにかかわらず生じます。
定在波とは、進行波と反射波が重なった混合波の振幅(包絡線、エンベロープ)の分布、またはその2乗であるパワーの分布であり、混合波そのものではありません。混合波は実在の波ですが、定在波はそのエンベロープであって、実在する波ではありません。
定在波を利用した測距 ― 定在波レーダ
■定在波レーダの基本構成
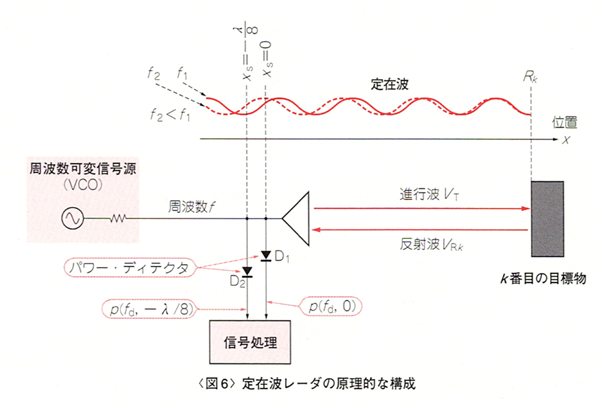
図6に定在波レーダの構成を示します。ほかのレーダに対して極めてシンプルな構成となっています。このためほかのレーダに比べて安価であることも特徴の一つです。
信号源は周波数を電圧制御できる発振器(VCO)です。VCOとアンテナをつなぐ線路上またはアンテナ給電部には、送信信号(進行波)と受信信号(反射波)が混在し、それらの干渉によって定在波が生じます。
VCOを制御し、周波数を切り替えながら、複数の周波数に対する混合波の信号レベルを検波器によって計測します。ただし、周波数を切り替えてから定在波が生じるまで、つまり少なくとも信号が目標物に反射して返ってくるまでの時間は、周波数を一定に保たなければならないため、必然的に周波数はステップ状に変化させる必要があります。
周波数に対する振幅の情報を信号処理することによって距離を算出します。ここで重要なことは、信号レベル計測のための検波器への分岐部分の考え方です。混合波の一部を分配して検波器へ導くのですが、このときカップリングは方向性を持ったものではなく、単純な無方向性のカップリングでなければなりません。後述しますが、定在波レーダにおいては「送信波の大きさ≫反射波の大きさ」であることが必要です。方向性カップリングを使って送信波を減衰させると、この条件が成立しなくなります。
■測距の原理
図6に示す信号源から出力される送信信号(進行波VT)が、
次式で表されるものとします。
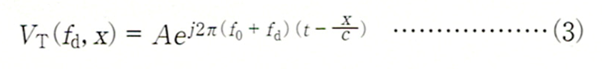
ただし、fd: f0からの周波数偏移[Hz] (−fw/2<fd<+fw/2), A: 振幅[V]、f0: 中心周波数[Hz]
また、x軸上の任意の一点をx=0 としています。
ここでk番目の目標物の位置をRk、反射係数の大きさと位相をそれぞれ γk,ϕkとすれば、そのターゲットからの反射波は次のように表すことができます。
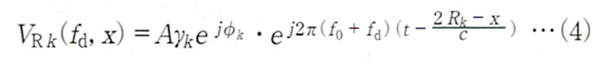
このとき、x=xsの位置に置いた検波器の出力、つまり混合波の振幅は ∣VT+∑VRk∣ なので、振幅の2乗、つまりパワーを p(fd,xs) とすれば、
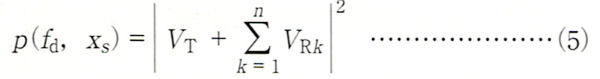
ここで「送信波の大きさ ≫ 反射波の大きさ」つまり
γk≪1の条件の下では、p(fd,xs) は次のように表すことができます。
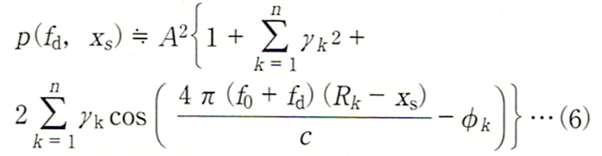
式(6)の第1項は送信波の電力、第2項は反射波の電力、第3項が定在波によって生じた成分です。一般のレーダは反射波(電力γk2)を受信し信号処理を行いますが、定在波レーダでは第3項を使います。第3項の振幅は2γkで、γk≪1であれば明らかに2γk≫γk2なので、ほかのレーダに比べて定在波レーダの方がSN比のよい信号を得ることができます。これは、レーダ断面積の小さい、つまり反射の少ない目標物や遠方の目標物に対して有効な性質です。
式(6)の第1項、第2項は不要なので、fdで微分することにより除去します。
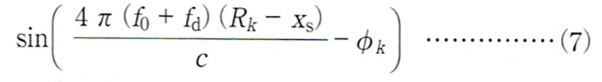
ここで検波器1の位置を原点(xs=0)とします。したがってdkは、検波器1から目標物までの距離となります。
また検波器2の位置をxs=−λ/8とすれば、各検波器からはそれぞれ次のような信号が得られます。
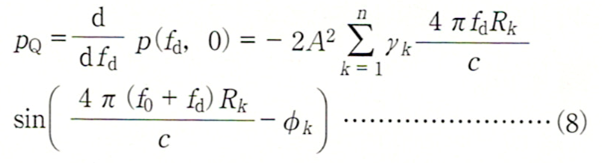
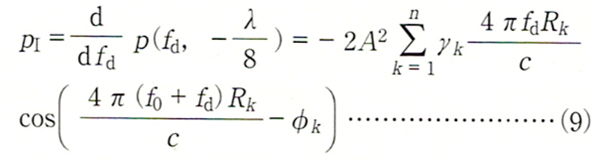
pI, pQにより次の複素信号を構成します。
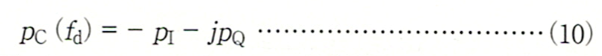
図7に、x=Rのところに目標物が一つ存在する場合のpC(fd)の実数部および虚数部を示します。
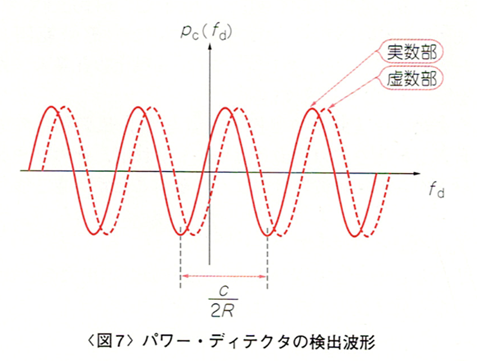
このようにpC(fd)は fdに関して周期関数であり、その周期は目標物の距離Rに逆比例していることがわかります。このことから、pC(fd) をフーリエ変換することによって、fd軸上の周期の逆数(周波数)である距離Rを求めることができます。つまり、
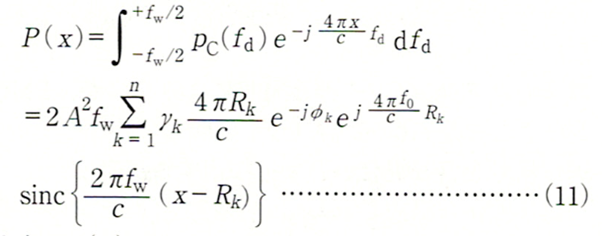
によりpC(fd)のフーリエ変換 P(x)が求められ、その絶対値を「距離スペクトル」と呼ぶことにします。
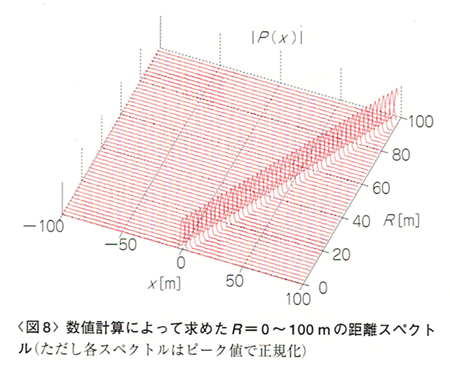
数値計算によって求めたR=0∼100 mの距離スペクトルを図8に示します。
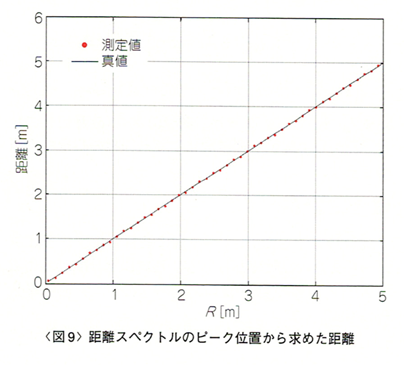
真の距離に対して、距離スペクトルのピーク位置から求めた距離をプロットしたものを図9に示します。このように定在波レーダは0mに近い至近距離から測距可能です。
■周波数の掃引を連続的にーリニアFM型定在波レーダ
定在波レーダにおいて、信号源の周波数をステップ状ではなく、連続的に変化させることを考えます。
周波数を連続的に変化させると、送受信信号の周波数が異なり、送受信信号が干渉しても厳密には定在波は生じないので、定在波レーダという名前は適当でないかもしれません。ただ、基本的な概念は同じなので、「リニアFM型定在波レーダ」と呼ぶことにします。信号源はFMCWレーダと同じになりますが、FMCWレーダとの違いは、受信信号を分離して検出しないで、送信信号を含む混合波として検出する点です。
信号源から出力される信号(送信信号)を瞬時周波数fが、

で表される、次のようなリニアFM信号とします。
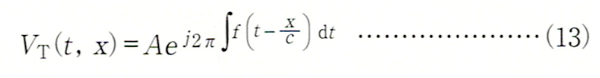
ただし、tは時刻、twは周波数がfw変化するのにかかる時間、f0は中心周波数、Aは振幅、cは光速です。またfdは中心周波数からの偏移で、その範囲は −fw/2<fd<+fw/2です。なお、x軸上の任意の一点をx=0としています。
このときk番目の目標の位置を Rk、反射係数の大きさと位相を γk,ϕkとすれば、そのターゲットからの反射波は次のように表すことができます。
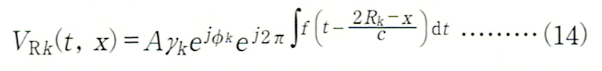
このとき x=xsの位置に置いた検波器の出力の2乗、つまり混合波のパワーは γk≪1として、
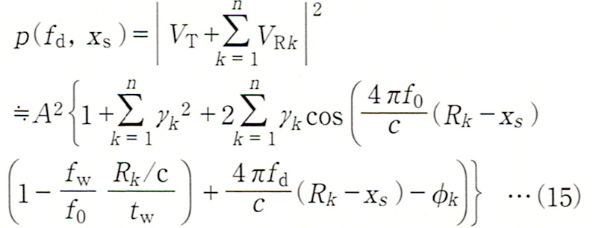
fw≪f0,Rk/c≪twならば、式(15)は式(6)と同じになり、周波数の掃引を連続的にしても同様の処理で測距できます。
■変位計測
式(11)で示したP(x)の位相に注目します。目標物が一つまたは複数であっても、互いに十分離れている場合、k番目の目標物に対応するスペクトル成分Pk(x) は、
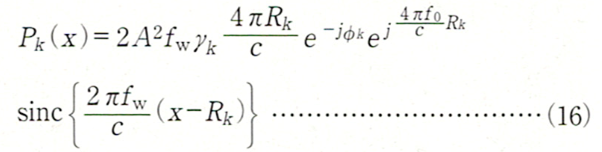
その位相 ψkは、

距離 Rkの変化分(変位)を Δdk、位相の変化分を Δψkとすれば、

これにより変位が求められます。
Δψk=πは、Δdk=c/(4f0)に相当します 。マイクロ波を使えば、例えば f0=24GHzでは、Δdk=3.125mmとなり、高い感度で変位を検知することが可能です。
技術評価用定在波レーダの概要
前出の写真1で示した技術評価用定在波レーダの仕様を表1にまとめておきます。24GHz帯特定小電力機器の規格に適合するように考慮されています。
ただし、このレーダは技術評価用、つまり製品化のための評価検討用素材なので、仕様はあくまで一例です。
投稿者注)
現在はSSRU-2401はコアデバイスであるフリーランVCO型のRFモジュール(IVS-465 / InnoSenT GmbH) の生産終了に供給を終了致しました。
PTMでは上位互換の設計思想にて次世代モデルを供給しています。(下記リンクにて製品ページへ)
高精度測距型(High Accuracy 1D) PSR24MTR11
位相モノパルス方位探知対応型(Monopulse 2D) PSR24MTR12
主な仕様について
周波数 24GHz帯(同等)
占有帯域幅 200MHz(法改正にて画期的に性能向上)
変調技術 フラクショナルPLL採用により高精度な周波数管理を実装
■構成
図10に評価用レーダのブロック図を示します、写真2は信号処理基板です。信号源(24GHz帯VCO)には、アンテナが一体となった写真3のようなモジュール(IVS-465)を使用しています。 このモジュールには二つの検波器も内蔵されています。
二つの検波信号はAC結合アンプで増幅され、A-Dコンバータに入力されます。またD-Aコンバータによって周波数制御信号を生成し、OPアンプを経由して、VCOの制御入力に加えます。


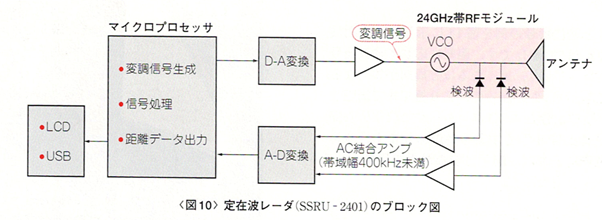
マイクロプロセッサは、変調信号の生成と信号処理(おもにFFT)を行います。
■実動作
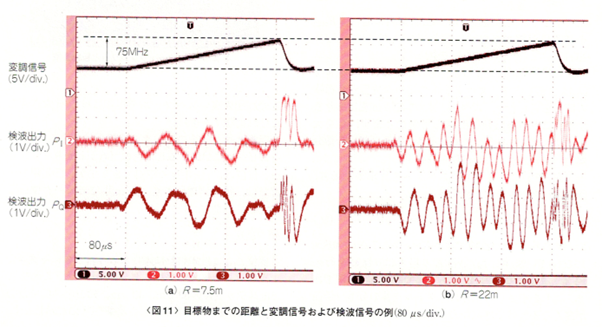
変調信号と検波信号の例を図11に示します。周波数の掃引幅fwは75MHzです。距離に応じて検波信号の周期が変わり、遠くなるほど周期が短くなるのが確認できます。したがって、より遠くまで測距する場合は、検波信号をA-Dコンバータで取り込む際のデータ間隔Δfを小さくする必要があります。サンプリング定理によれば、測距可能な最大の距離Rmaxは、

となります。信号処理上は、Δfを適当に選べば Rmaxを任意に設定できます。評価用レーダでは、Δf=293 kHzで Rmax=256mです。
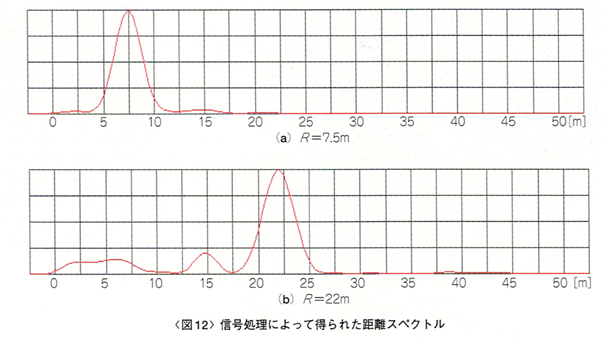
次に、信号処理によって得られた距離スペクトルを図12に示します。 スペクトルのピーク位置が目標物の距離を表します。スペクトルの幅が5m程度ありますが、これは周波数掃引幅fwで決まります。
fwを大きくすればスペクトルの幅は小さくなり、鋭く分離分解能の高いスペクトルが得られます。
N点FFTによって距離スペクトルを求めた場合、距離スペクトルのデータ間隔Δxは、

で与えられます。図12では、N=1024でΔx=0.5mとなっています。fw/Δf<Nの場合は0埋めを行いFFTします。なお、Δxはあくまで計算上の間隔であり、これを小さくしてもスペクトル自体の分離分解能が高くなるわけではありません。前述したように、分離分解能の高いスペクトルを得るにはfwを大きくしなければなりません。
距離スペクトルのピークの位置を推定することで、そのピークに対応する目標物の距離がわかります。ピーク位置は、Δx単位で推定できますが、評価用レーダでは、補間処理により、1cm単位でピーク位置を推定しています。
■変位
変位Δdkは、式(18)により求められます。写真4のようなコーナー・リフレクタを目標物とし、これを10µmステップで、30µm、40µm、50µmの幅で前後に動かし、その変位を測定した結果を図13に示します。

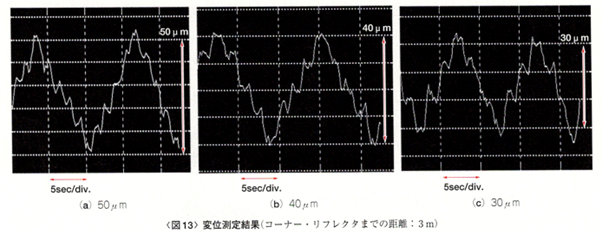
コーナー・リフレクタの揺れが含まれているため、少々わかりにくいのですが、10µmステップで目標物が動いていることが確認できます。
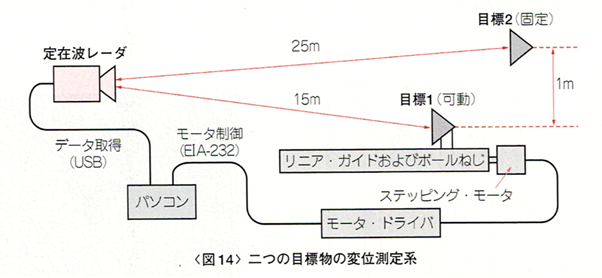
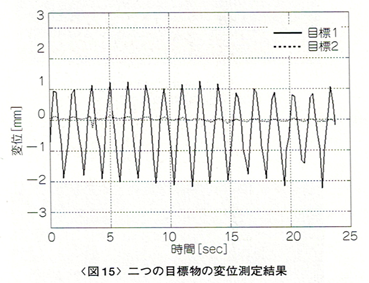
次に図14のように複数(二つ)の目標物を置き、一つを固定、もう一つを前後に3mm動かしました。図15に示す結果からわかるように、各目標物の変位を個別に計測できていることがわかります。
応用例
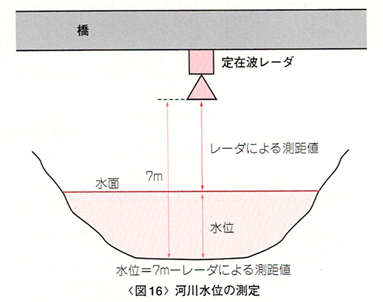
■水位の計測
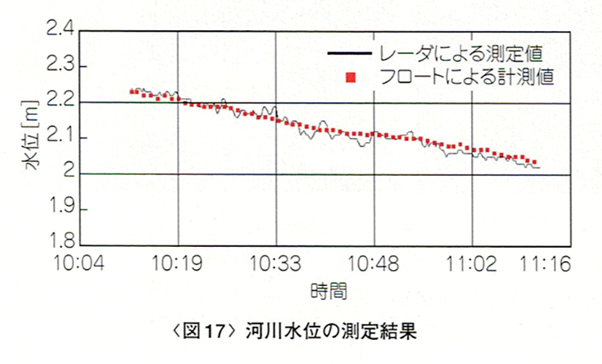
水面の上、数mに定在波レーダを設置し、河川の水位を計測します。増水時はレーダから水面までの距離が短くなるので、近距離測定ができる必要があります。
図16のようにレーダを水面からおよそ5mの位置に設置し、川底からレーダまで距離(約7m)からレーダの測距値を引き、水位を求めた結果を図17に示します。水面は常に揺らいでいるため、測定値に対して移動平均処理を行っています。フロートによる目視の計測値とほぼ一致しています。
■心拍・呼吸の検知
人の心拍数は、安静時には1分間に50~95回(0.83 Hz~1.58Hz)、呼吸数は1分間に16~25回(0.27Hz~0.42Hz)程度とされています。(日本薬学会編:「知っておきたい臨床検査値」(株)東京科学同人)
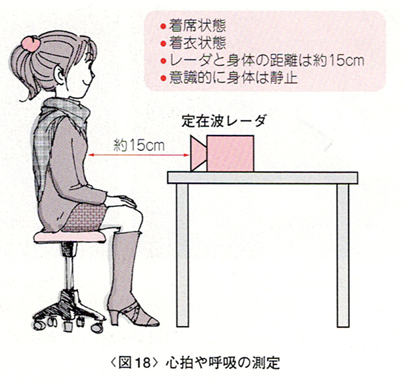
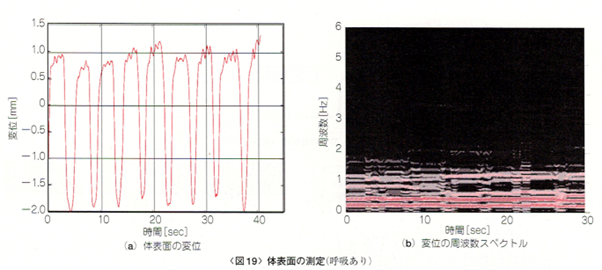
図18のように定在波レーダを胸部の前15cm程度の位置に置き、心拍・呼吸による体表面の変位を計測します。図19(a)は呼吸状態で変位を計測した結果です。呼吸によるものと思われる振幅の大きな周期成分が見られます。これを短時間FFTしたものを図19(b)に示します。0.2~0.3 Hz辺りに呼吸によるものと思われる成分が確認できます。ほかの主な成分は、その高調波と考えられます。心拍の成分も存在するはずですが、呼吸の成分の高調波に埋もれてしまい、はっきりと識別することはできません。
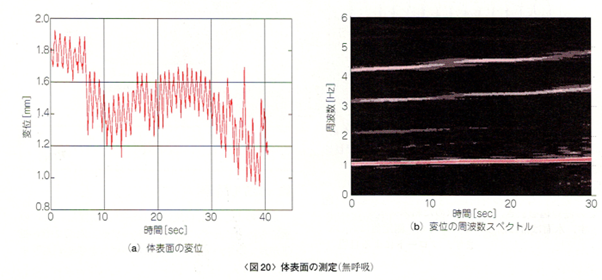
次に呼吸を止めた場合の変位を図20(a)に示します 。心拍によると思われる変位の周期的変化がみられます。これを短時間FFTしたものを図20(b)に示します。1Hz辺りに心拍の成分が確認できます。
■人・車の検知
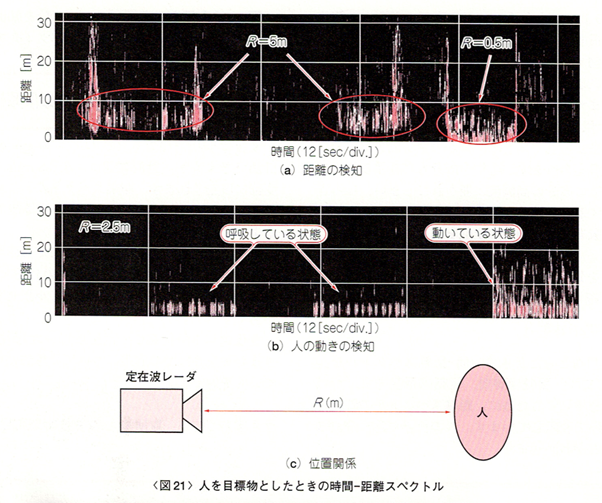
人を目標物としたときの時間-距離スペクトルを図21に示します。横軸は時間、縦軸は距離です。ただし、動きを検知するために、距離スペクトルの時間変化分(微分)を表示しています 。人の位置や動きが検知できることがわかります。
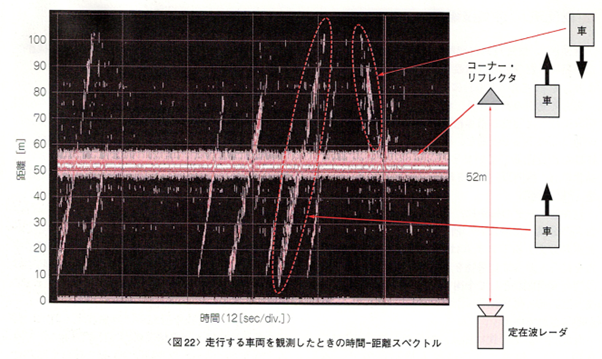
図22は走行する車両(普通自動車)を観測したときの(微分していない)時間-距離スペクトルです。車両の動きを明確に観測できています。
技術的課題と今後の展開
変位は位相情報をもとにして、10µmの分解能で計測できますが、計測範囲は±3.125mm以内の相対変位に限定されます。距離スペクトルと位相を組み合わせて、距離そのものを10µmの分解能で計測できるような手法を検討しています。
定在波レーダのハードウェアとしては、今回紹介したものはあくまで一例です。基板設計にもよりますが、回路規模は大きくないので、さらに小型化することは容易です。
今後は、本技術を広く活用していただけるように、さまざまな分野での応用について具体的に検証を行っていく予定です。
著者紹介:
上保 徹志 うえぼ てつじ