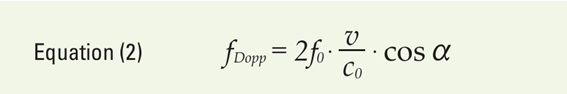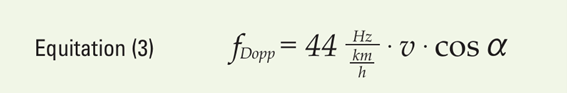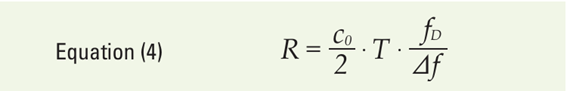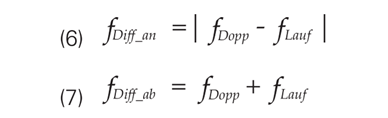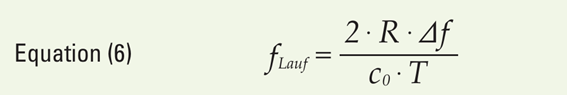3 レーダー方式の選択
レーダー方式は大きく2種類に分類されます。
- CW(連続波)レーダー
- パルスレーダー
どちらを選択するかは対象アプリケーションに依存し、測定したいパラメータが何かによって決まります。
- 物体の存在および動き
- 距離(レンジ)
3.1.移動物検出:CW(無変調式)レーダー(ドップラー方式)
3.1.1 基本構成要素
移動目標の検出だけを重視されるアプリケーションではCW(無変調)ドップラー方式が最も有効かつ簡単な解決策となります。
この方式は「ドップラー効果」を活用しています。ドップラー効果とは、物理現象におけるすべての「波」について説明されており、概要は以下のとおりです。
音波、マイクロ波、光などの波源から発せられた波面が、移動中のターゲット(物体)に到達すると、その物体の移動方向に応じて波面が「圧縮」されたり「引き延ばされたり」します。この現象は、最終的に周波数の変化、すなわち周波数シフトとなって現れます。
このようにして周波数が変化し、反射された信号は、変化していない送信信号と比較的単純なミキサ(無線工学では「ホモダイン混合器」など呼ばれる)で混合されます。
これにより正弦波状の中間周波数(IF: Intermediate Frequency)信号が得られます。なお、センサが物体に対して移動している場合でも、物体がセンサに対して移動している場合でも同じ結果が得られます。
実際に計算できるのは、センサと物体を直接結ぶ直線方向に沿った速度ベクトルの成分だけです。
この現象は次のような公式で表されます:
公式2 ドップラー方程式
ここで
fD:ドップラー周波数(差動周波数)
f0:レーダー送信周波数
v :移動物体の速度大きさ
c0:光速
α :移動方向とセンサ-物体接続線のなす角度
公式3 送信周波数を24 GHzとした場合のドップラー周波数と速度の関係:
この式により速度とドップラー周波数の関係は容易に計算可能で、後段のIFアンプに必要な通過帯域も予測できます。
例えば、人の検出を目的としたセンサの信号処理部の上限周波数を300Hzより高く設計する意味はほとんどありません。これは約時速6.8km(速歩)に相当します。
一方、ドイツの高速道路(Autobahn)で車両速度を計測する場合は、少なくとも10kHzまで処理できるアンプが必要であります。これは時速220kmに相当します。
すなわち、物体の速度はドップラー周波数(アナログシステムではゼロクロッシング数、デジタルシステムではFFT処理)を計測し、運動ベクトルの角度を考慮して評価されます。
注意:
非常にまれなケースとして、物体がセンサーの周囲を完全な円運動で移動する場合、角度が 0° となり、その結果、cos(余弦)が 0 となってドップラー周波数もゼロになります。このような特定の動きは、このタイプのレーダーでは検出できません。
ただし、このような物体は、完全な円の軌道上を完璧に動く必要があり、現実的には物体は体積を有する為、そのような動作はほとんどあり得ません。
よく知られる(一方である意味「嫌われる」)例として、警察の速度取締り用レーダーがあります。これらは一定かつ特定の角度に厳密に合わせて設置されており、対象車両の速度検出を実現しています。
信号処理部については本ノート後半で詳述します。
3.1.2 運動方向の識別
レーダーセンサは、運動方向(接近か離脱か)を判別可能な大きな利点を持ちます。
これは、位相差が90°異なるミキサ(I/Qミキサ)を設けることで実現しています。
多くの応用では、人物接近時にドアを開けたり、蛇口・小便器からの退去後に排水を促したりといった方向判別に基づく制御が求められます。
I/Q信号の位相関係から、物体の接近か離脱かを判定します。レーダーセンサは、運動方向(接近か離脱か)が判別可能になる事で大きな優位性をもたらします。
3.2 静止物体の検出
3.2.1 パルスレーダー
移動・静止を問わず、「物体の位置、すなわち距離」の計測が主要目的の場合、パルスレーダーは非常に原理的な解決策と言えます。
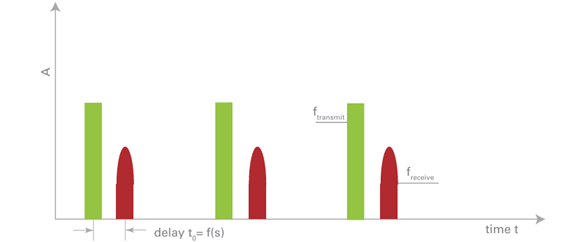
図1:パルスレーダーの送受信信号の時間変化
パルスを短く送信し、それが反射されて戻るまでの時間遅延を計測するという非常に原理的な方式です。
光速で移動するパルス群は、対象物体までの片道距離の2倍を進みます。例えば対象が1m先の場合、パルスは約6ナノ秒遅れて反射波が戻ってきます。
短パルス技術については多くのの課題が存在します。
特に近距離物体を高分解能で検出しようとすると、パルス幅を非常に短くする必要があり、それに伴い必要帯域幅が膨大になります。これは多くの電波法上の制約を全う出来なくなる為、多くの場合認可されません。
また、パルスレーダーは主に距離測定に特化しており、速度情報は多点での距離測定値を時間領域での微分による推定でしか推定できません。
3.2.2 FMCW レーダー(距離測定専用)
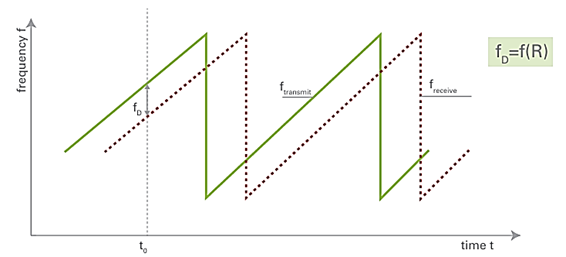
図2:鋸波(SAWTOOTH)変調方式FMCWレーダーの送受信信号時間変化
FMCW(周波数変調連続波)レーダーは、静止している物体を検出するために、パルス方式とは異なるアプローチを提案します。
FMCW方式では電磁波を連続的に送信しますが、その周波数は時間の関数として変化します。送信された信号は、反射により時間遅延を受けるため、遅延を伴った送信信号(すなわち反射信号)と、現在の送信信号では瞬間的な周波数値がわずかに異なります。これは、送信周波数がその間に進行して変化しているためです。
最も単純な方法として時間とともに周波数を変化させる鋸波(SAWTOOTH)制御により、図2に示す様な制御を実装します。
この時、距離と差動周波数の関係は以下の式で表されます:
公式4 距離値演算式
ここで
fD:周波数差分
⊿f:周波数偏移
T :チャープ時間
R :反射体までの距離
c0:光速
24GHz帯の場合、最大200 MHzの帯域幅(周波数変調幅)が認められており、簡単な処理では最小検出距離がおおよそ2~3 mとなります。
これより近距離を測ろうとすると、高速かつ複雑なDSP(デジタル信号処理)やFPGAなどが必要になります。
一方で、このレーダーはあいまいさのない広い測定領域(ゾーン)を持っています。これは、のこぎり波の繰り返し時間 Tを必要に応じて十分に長く設定できるためです。
3.3 距離と速度の同時測定
3.3.1 FSK レーダー
FMCWレーダーとは異なり、送信周波数を単調に変化させる代わりに、数MHzまたは数十MHzの差を持つ2つの周波数間で切替えを行います。(2周波ドップラーともいわれます)
この切替時に受信信号の位相差を解析することで、瞬時距離を求めることが可能です。
同時に、前節2.2.1.1で説明したドップラーシフトにより速度情報を獲得します。信号波形を保存して比較するか、位相比較器に入力するのが推奨されます。
距離は以下の式から算出可能です:
ここで
- F1, F2:送信の2周波数
- c0:光速
- φ1,φ2:ミキサ出力信号の位相差(ラジアン)
- R:距離
3.3.2 トライアングル型(三角波変調)FMCW レーダー
数学的な観点から見ると、物体の速度と距離を計算することは、2つの未知数を持つ方程式系を解くことを意味します。明確な解を得るためには、2つの異なる方程式が必要です。
ターゲットの移動が受信信号の周波数を上下にシフトさせ、一方でターゲットまでの距離が、時間遅延によって信号を時間軸方向に平行移動させることを確認しています。
したがって、送信周波数の形状をあらかじめ適切に選ぶことで、受信後に速度と距離の両方を確実に取り出せるようにすることは論理的に可能です。
それは必ずしも最初のステップで得られるとは限りませんが、単純な追加の数学的処理によって確実に抽出することができます。
このアプローチに対してトライアングル型(三角波)変調が用いられます。
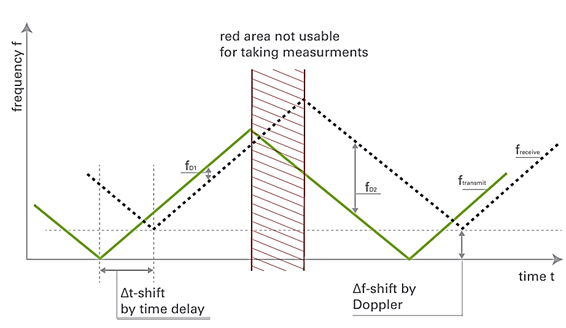
図3:三角波変調のFMCWレーダー送受信信号時間変化
アップチャープ(周波数上昇区間)では、移動に伴うドップラー周波数シフトと距離に起因する遅延効果が打ち消し合い、ダウンチャープ(周波数下降区間)では、両者が加算されます。
ここで
- f{D1}:アップチャープにおけるビート周波数(測定値)
- f{D2}:ダウンチャープにおけるビート周波数(測定値)
- f{Doppler}:移動体によるドップラーシフト周波数(式(2)参照)
- f{delay}:距離による遅延効果に起因する周波数シフト(式(4)参照)
理想的で完全に直線的な周波数変化、すなわち三角波状のチャープがあると仮定すると、掃引周波数の増加部分および減少部分の両方において、周波数差が完全に一定となる特定の時間間隔が存在します。これを信号処理に活用する事が可能です。
得られた差周波数を評価した後、速度 v と距離 R を求めるために式(6)と(7)を加算および減算する必要があります。
差周波数の処理には注意が必要です。なぜなら、図3に赤くハッチされた領域は信号波形が不安定であるため使用できず、処理から除外すべきだからです。